信息安全技术数学基础
数论
因子
-
因子(定义)
设$a, b ∈ Z$,$a ≠ 0$,$c ∈ Z$,使得$b = ac$,则称$a$整除$b$,并称$a$是$b$的因子或者约数,$b$是$a$的倍数,记为$a | b$。
如果整数$a$除整数$b$得到的商$c$是整数,那么称$a$是$b$的因子/约数,$b$是$a$的倍数,记为$a | b$。
有如下性质:
- $a|a$
- 如果$a|b$,$b|c$,那么$a|c$成立
- 如果$a|c$,那么$ab|cb$成立
- 如果$a|b$,$a|c$,那么对于任意整数x、y,$a|(bx+cy)$成立
- 如果$a|b$,$b|a$,那么$a=\pm b$
-
带余除法(定理)
设$a, b ∈ Z$,$b ≥ 1$,则存在唯一的整数$q$和$r$,使得$a = qb + r$,$0 ≤ r < b$。$q$称$a$除以$b$所得的商,$r$称为$a$除以$b$所得的最小非负剩余。
$a$为整数,$b$为正整数,那么$a = qb + r$可以确定唯一的$q$(商)和$r$(最小非负剩余,一定小于$b$)。
-
最大公因子(定义)
设$a, b ∈ Z$,$a,b$不全为0,如果$c | a$且$c | b$,则称$c$为$a$和$b$的公因子。特别地,我们把$a$和$b$的所有公因子中最大的,称为$a$和$b$的最大公因子,记为$gcd(a,b)$ 或者 (a, b)。
如果$c$为不都为0的整数$a$、$b$的因子,那么$c$为$a$、$b$的公因子,其中最大公因子记作$gcd(a,b)$或$(a,b)$。
-
欧几里得算法(定理)
给定整数$a$和$b$,且$b>0$,重复使用带余除法,即每次的余数为除数去除上一次的除数,直到余数为0,这样可以得到下面一组方程:
$a = bq_1+r_1$,$0 < r_1 <b$
$b = r_1q_2+r_2$,$0 < r_2 < r_1$
$r_1 = r_2q_3+r_3$,$0 < r_3 < r_2$
……
$r_{j-1} = r_jq_{j+1}$
最后一个不为0的余数$r_j$就是$a$和$b$的最大公因子
欧几里得算法求$gcd(a,b)$:第一次将两数作为$a$和$b$进行带余除法($a = qb + r$),在下一次带余除法计算时$b$作为$a$,余数$r$作为$b$,多次计算直到余数为0的$r_j$即最大公因子。
求$gcd(1970,1066)$
求$gcd(1970,1066)$:
$1970 = 1 × 1066 + 904$
$1066 = 1 × 904 + 162$
$904 = 5 × 162 + 94$
$162 = 1 × 94 + 68$
$94 = 1 × 68 + 26$
$68 = 2 × 26 + 16$
$26 = 1 × 16 + 10$
$16 = 1 × 10 + 6$
$10 = 1 × 6 + 4$
$6 = 1 × 4 + 2$
$4 = 2 × 2 + 0$
因此$gcd (1970,1066) = 2$
-
推导定理
对任何非负整数$a$和正整数$b$,有$gcd(a,b)=gcd(b, a\bmod b)$。
-
素数
-
素数(定义)
设$p ∈Z$,$p≥2$,如果$p$的正因子只有1和$p$,则称$p$为素数,否则为合数
素数的因子只有1和其本身。
性质:
- 数字越大的区间素数分布越稀疏,对于每个大于等于2的整数$n$,连续$n-1$个整数$n!+2$,$n!+3$,$\dots$,$n!+n$都不是素数
- 任意两个相邻的正整数$n$和$n+1$($n>3$)中必有一个不是素数
- $n$和$n+2$均为素数的数对称为孪生素数,例如$(3,5)$,$(5,7)$,$(11,13)$,$(29,31)$。
-
素因子(定义)
若正整数$a$有一因子$b$,而$b$又是素数,则称$b$为$a$的素因子
数的因子也是素数,那么该因子成为素因子。
-
推导定理
若$a$是大于1的整数,则$a$的大于1的最小因子一定是素数。
本定理说明了任何大于1的整数均可被一素数整除,或者说都至少有一素因子。
-
性质:
- 如果$p$是素数,且$p|ab$,则$p|a$或$p|b$
- 对于任意大于1的整数$m$,都有唯一分解式:$m=p_{1}^{a_1}p_{2}^{a_2}\dots p_{n}^{a_k}$,其中$p_1$,$p_2$,$\dots$,$p_n$均为素数,$p_i>p_j(i<j)$,且$a_i$都是正整数
- 素数个数有无穷多个
-
素数定理:
设$\pi(x)$表示不大于$x$的素数的数目,则$\lim_{x \to \infty}\frac{\pi(x)\ln x}{x}=1 $。
素数定理表明,对充分大的$x$,$\pi(x)$可用$\frac{x}{\ln x}$近似表示
-
-
互素(定义)
如果整数$a$与整数$b$的最大公因子是1,即$gcd (a, b) = 1$,则称$a$与$b$互为素数,简称互素
互素的正整数中不一定有素数,例如$gcd(25,36)=1$,但25和36均为合数。
-
欧拉函数(定义)
设$\varphi (m)$为小于或等于$m$且与$m$互素的正整数个数,则称其为欧拉(Euler)函数
欧拉函数举例
$\varphi(1)=1$:1
$\varphi(2)=1$:1
$\varphi(3)=2$:1、2
$\varphi(5)=4$:1、2、3、4
$\varphi(8)=4$:1、3、5、7
同余
用$Z_m$表示正整数{$0,1,\dots,m-1$}的集合
-
模数(定义)
两个整数$a$, $b$分别被$m$除,如果所得的余数相同,则称$a$与$b$对模$m$是同余的,记为$a\equiv b(\bmod m)$,正整数$m$称为模数。
性质:
- $a\equiv b(\bmod m) \Leftrightarrow m|(b-a)$
- 如果$a=km+b$(k为整数),则$a\equiv b(\bmod m)$
- 每个整数恰与0,1,…,$m-1$这$m$个整数中的某一个对模$m$同余
- 同余关系是一种等价关系
- $a\equiv b(\bmod m)$当且仅当$a \bmod m = b \bmod m$
同余式性质:
(若$a\equiv b(\bmod m)$,$c\equiv d(\bmod m)$)
- 同余式可加:$ax+cy\equiv bx+dy(\bmod m)$
- 同余式可乘:$ac\equiv bd(\bmod m)$
- $an\equiv bn(\bmod m)$,$n>0$
- $f(a)\equiv f(b)(\bmod m)$,$f(x)$为任意一个整系数多项式
(若$a$,$b$,$c$,$d$为整数,$m$为正整数)
- 若$a\equiv b(\bmod m)$,且$d|m$,则$a\equiv b(\bmod d)$
- 若$a\equiv b(\bmod m)$,则$gcd(a,m)=gcd(b,m)$
-
乘法消去律(定理)
对于$ab\equiv ac(\bmod m)$来说,若$gcd(a,m)=1$,则$b\equiv c(\bmod m)$。
对于$ab\equiv ac(\bmod m)$,若$a$、$m$互素,则可直接消去$a$。
-
加法消去律(定理)
如果$a+b\equiv a+c(\bmod m)$,则$b\equiv c(\bmod m)$。
-
剩余类/同余类(定义)
由于模$m$同余关系是一个等价关系,若将$Z$中的同余的树归为一类,不同余的数归为不同的类,则将$Z$分为$m$个类,称为模$m$的剩余类或同余类。
按照$Z$对$m$取模的余数将数划分为不同的类,称为剩余类(同余类)。
使用$[r]$表示$r$所属的模$m$的剩余类($r \bmod m$)
-
非负最小完全剩余系(定义)
在模$m$剩余类$[0],[1],\dots,[m-1]$中各取一数$a_0,a_1,\dots,a_{m-1}$,该m个数$a_0,a_1,\dots,a_{m-1}$称为模$m$的一个完全剩余系,将{$0,1,\dots,m-1$}记为$Z_m$,称为模$m$的非负最小完全剩余系。
-
简化剩余系(定义)
若模$m$剩余类中的数与$m$互素,称它为与模$m$互素的剩余类,在与模$m$互素的所有剩余类中各取一数所组成的集合,称为模$m$的一个简化剩余系,$Z_m$的简化剩余系记为$Z^{*}_{m}$。
-
一次同余方程(定义)
若$a$、$b$都是整数,且$m$不能整除$a$,则称$ax\equiv b(\bmod m)$为模$m$的一次同余方程。
若$x_0$满足$ax_0\equiv b(\bmod m)$,则$x\equiv x_0(\bmod m)$称为它的解,其全部解可以表示为$x_0+mk, k=0,\pm 1, \pm2, \dots$。(不同解指的是互不同余的解)
-
一次同余方程有唯一解(定理)
设$a\in Z_m$,对于任意的$b\in Z_m$,同余方程$ax\equiv b(\bmod m)$有唯一解$x\in Z_m$的充分必要条件是$gcd(a,m)=1$
-
一次同余方程有解(定理)
设$gcd(a,m)=d,m\gt 0$,则$ax\equiv b(\bmod m)$有解,当且仅当$d|b$
模运算
-
性质
- $(a\pm b) \bmod m = [(a \bmod m)\pm (b\bmod m)] \bmod m$
- $(a\times b) \bmod m = [(a \bmod m)\times (b\bmod m)] \bmod m$
- $[a\times (b + c)] \bmod m = [(a\times b) \bmod m+ (b\times c)\bmod m] \bmod m$
-
加法逆元(定义)
对$a\in Z_m$,存在$b\in Z_m$,使得$a+b\equiv 0(\bmod m)$,则$b$是$a$的加法逆元,记$b=-a$。
加法一定存在逆元。
-
乘法逆元(定义)
对$a\in Z_m$,存在$b\in Z_m$,使得$a\times b\equiv 1(\bmod m)$,则称$b$是$a$的乘法逆元。
乘法不一定存在逆元。
在密码学特别是非对称密码体制中,常常需要求模逆元,求模逆元就是求乘法逆元。即寻找一个$x$,使得$a \times x \equiv 1 \bmod m$成立。模逆元不一定存在结果,通常试用欧几里得算法求出。
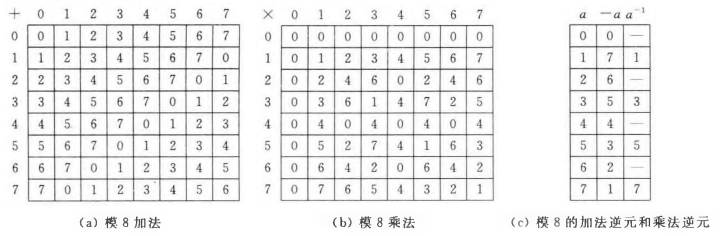
- 对应每个$x$都有一个对应的$y$使得$x+y\equiv 0 \bmod 8$,则$y$是$x$的加法逆元。如对2,存在加法逆元6使得$2+6\equiv 0 \bmod 8$。
- 对应$x$存在$y$使得$x\times y\equiv 1\bmod 8$,则$y$是$x$的乘法逆元。如对3,存在乘法逆元3使得$3\times 3\equiv 1\bmod 8$。
-
快速指数模运算
求$m^e\bmod n$的方法
-
常规算法
原理:模运算性质$(a\times b) \bmod m = [(a \bmod m)\times (b\bmod m)] \bmod m$
变换:$a^e\bmod m = [(a \bmod m)^e]\bmod m$
-
快速求法
- $a\gets e$,$b\gets m$,$c\gets 1$, 其中$a$,$b$,$c$为三大整数寄存器。
- 如果$a=0$,则输出结果$c$即为所求的模n的大整数次幂。
- 如果$a$是奇数,转第5步。
- $a\gets \frac{a}{2}$,$b\gets b\times b\bmod n$,转第3步。
- $a\gets (a-1)$,$c\gets (c\times b) \bmod n$,转第2步。
计算$30^{37}\bmod 77$
a b e 37 30 1 36 与前一次值相同 $(30\times 1)\bmod 77=30$ 18 $(30\times 30)\bmod 77=53$ 与前一次值相同 9 $(53\times 53)\bmod 77=37$ 与前一次值相同 8 与前一次值相同 $(37\times 30)\bmod 77=32$ 4 $(37\times 37)\bmod 77=60$ 与前一次值相同 2 $(60\times 60)\bmod 77=58$ 与前一次值相同 1 $(58\times 58)\bmod 77=53$ 与前一次值相同 0 与前一次值相同 $(53\times 32)\bmod 77=2$ 得$c=2$,即$30^{37}\bmod 77=2$
-
费马定理和欧拉定理
-
费马定理(定理)
若$p$是素数,且$a$是正整数,且$gcd(a,p)=1$,则$a^{p-1}\equiv 1(\bmod p)$。
例$a=7,p=19$
$a=7,p=19,gcd(a,p)=1$
$7^2=49\equiv 11\bmod 19$
$7^4\equiv 121\bmod 19\equiv 7\bmod 19$
$7^8\equiv49\bmod 19\equiv 11\bmod 19$
$7^{16}\equiv 121\bmod 19 \equiv 7 \bmod 19$
$a^{p-1}=7^{18}=7^{16}\times 7^2\equiv 7\times 11\bmod 19\equiv 1\bmod 19$
推论(费马定理另一种总表现形式):
设$p$是素数,对于任意正整数$a$,则$a^p\equiv a(\bmod p)$。
推论不要求$gcd(a,p)=1$,即$a,p$互素
-
欧拉定理(定理)
对于任意互素的两个整数$a,n$,有:$a^{\varphi (n)}\equiv 1\bmod m$。
欧拉定理举例
$a=3,n=10$:$\varphi (10)=4,a^{\varphi(n)}=3^4=81\equiv 1\bmod 10=1\bmod n$
$a=2,n=11$:$\varphi(11)=10,a^{\varphi (n)}=3^{10}=1024\equiv1\bmod 11=1\bmod n$
对于欧拉定理,有:
- 当$n=p$时,有$a^{p-1}\equiv 1\bmod p$,为费马定理
- 易见$a^{\varphi (n+1)}\equiv a\bmod n$(欧拉定理的另一种形式不要求$a$和$n$互素)
求$13^{2001}$被$60$除所得的余数
$\because gcd(13,60)=1$
$\therefore 13^{\varphi (60)}\equiv 1(\bmod 60)$
$\because \varphi (60)=\varphi (2^2\times 3\times 5)=2\times(3-1)\times(5-1)=16$,$2001=125\times 16+1$
$\therefore 13^{16}\equiv 1(\bmod 60)$,$13^{2001}=(13^{16})^{125}\times 13\equiv 13(\bmod 60)$
即被60除所得的余数为13
素性测试
素性测试即检验一个大数是否为素数,通常用于密码算法中需要大素数时判断随机生成的数是否为素数。
如果$p$为大于2的素数,则方程$x^2\equiv 1(\bmod p)$的解只有$x=1$和$x=-1$。
定理的逆否命题为:如果方程$x^2\equiv 1(\bmod p)$有一个解$x_0\notin$ {$-1,1$},那么p不是素数。
Miller-Rabin素性概率检验算法
1 | public class MillerRabinTest { |
算法有两个输入,$n$是待检验的数,$a$是小于n的整数。如果算法的返回值为TRUE,则$n$肯定不是素数,如果返回值为FALSE,则$n$有可能是素数。
for循环后,有$d = a^{n-1}\bmod n$,由费马定理可知,若$n$为素数,则$d$为1,因此若$d\ne 1$,则$n$不是素数,所以返回TRUE。
因为$n-1\equiv -1\bmod n$,所以$x\ne 1$,$x\ne n-1$,表示$x^2\equiv 1 (\bmod p)$有不在{$-1,1$}中的根,因此$n$不为素数,返回TRUE。
中国剩余定理
设$m_1,m_2,\dots ,m_k$是两两互素的正整数,令
上式中$M_i=\frac{M}{m_i},i=1,2\dots,k$,则同时满足同余方程组
的唯一正整数解$x_0$是:
上式中$M^{\prime}_{i}$是$M_i$以$m_i$为模的逆元。
求解$x$举例
求解满足以下方程的解$x$:
$x\equiv 1\bmod 2$ $x\equiv 2\bmod 3$ $x\equiv 3\bmod 5$ $x\equiv 5\bmod 7$
$M=m_1m_2m_3m_4=2\times 3\times 5\times 7=210$
$M_1=105,M_2=70,M_3=42,M_4=30$
由扩展欧几里得定理:
$\therefore x\bmod 210\equiv(1\times 105\times 1+ 2\times 70\times 1+3\times 42\times 3+5\times 30\times 4)\bmod 210\equiv 173$
即$x\equiv 173\bmod 210$
离散对数
-
本原根(定义)
若$Ord_na=\varphi (n)$,则称$a$是模$n$的本原根,也称生成元。
指数:假设$gcd(a,n)-1$,如果使$m$是使$a^m\equiv 1\bmod n$成立的最小正整数,则称它是$a$对模$n$的指数,记为$Ord_na$。
并非所有的整数都有本原根。模$m$的本原根存在的必要条件是$m=2,4,p^a$或$2p^a$,此处$p$为奇素数。
求模7和模15的本原根
对于模7:满足$gcd(a,n)=1$的$a$是{$1,2,3,4,5,6$},指数表如下:
$a$ 1 2 3 4 5 6 $Ord_7a$ 1 3 6 3 6 2 当$a=3$或$5$时,$Ord_7a=\varphi (7)$,因此3和5是模7的本原根。
对于模15:满足$gcd(a,n)=1$的$a$是{$1,2,4,7,8,11,13,14$},指数表如下:
$a$ 1 2 4 7 8 11 13 14 $Ord_{15}a$ 1 4 2 4 4 2 4 2 从上表中可以看出不存在$a$使得$Ord_{15}a=\varphi (15)$,所以模15没有本原根。
-
简化剩余系(定理)
若$a$是模$n$的本原根,则$1,a^1,a^2,\dots,a^{\varphi (n)}$构成模$n$的简化剩余系。
-
本原根的测试
令$q_1,q_2,\dots,q_n$是$p-1$的素因子,对于所有的$q_1,q_2,\dots,q_n$计算$a^{\frac{p-1}{q}}(\bmod p)$,如果对于某个$q$的某个值其结果为1,那么$a$不是一个本原根。如果对于某个$q$的所有值其结果都不为1,那么$a$是一个本原根。
假设$p=11$,检验2和3是否是一个本原根
当$p=11$时,$p-1=10$,$p-1$有两个素因子2和5
对2判断:
$2^{\frac{10-1}{5}}(\bmod 11)=4$ $2^{\frac{10-1}{2}}(\bmod 11)=10$ 由于计算结果没有1,故2是本原根。
对3判断:
$3^{\frac{10-1}{5}}(\bmod 11)=9$ $3^{\frac{10-1}{2}}(\bmod 11)=1$ 由于计算结果存在1,故3不是本原根。
-
离散对数
模运算用于指数计算可以表示为$a^x\bmod n$,称为模指数运算,其逆向问题就是找出一个数的离散对数,即求解$x$,使得:$a^x\equiv b\bmod n$。
对于一个整数$b$和素数$n$的一个本原根$a$,可以找到唯一的指数$x$,使得$b\equiv a^x\bmod n$,其中$0\le x\le n-1$,指数$x$称为$b$的以$a$为基数的模$n$的离散对数。
并非所有离散对数都有解。
例如取$n=11$,有3个本原根2、6、8
-
求模数:
当$a=2,x=9$可求出模数$b=6$
当$a=5,x=7$可求出模数$b=8$
当$a=8,x=4$可求出模数$b=4$
-
求离散对数:
当$a=2,b=3$可求出离散对数$x=8$
当$a=6,b=5$可求出离散对数$x=6$
当$a=8,b=10$可求出离散对数$x=5$
-
二次剩余
-
定义
如果$gcd(a,m)=1$,并且$2^x\equiv a(\bmod m)$有解,则称$a$是$m$的二次剩余(平方剩余),否则称$a$是$m$非二次剩余。满足$x^2\equiv a(\bmod m)$的$x$称为模$m$的一个平方根。
-
性质:
- 如果$m$是素数,则整数$1,2,\dots,m-1$中正好有$\frac{m-1}{2}$个是模$m$的二次剩余,其余的$\frac{m-1}{2}$个是模$m$的非二次剩余。
- 如果是$a$的模$m$的一个二次剩余,那么$a$恰好有两个平方根,其中一个在$0\sim\frac{m-1}{2}$之间,另一个在$\frac{m-1}{2}\sim m-1$之间。
- 如果$m$是两个素数$p$和$q$之积,那么模$m$恰好有$\frac{(p-1)(q-1)}{4}$个二次剩余,有$\frac{3(p-1)(q-1)}{4}$个非二次剩余。
- 当$m$是复合数时,如果$m$的分解未知,则求方程$x^2\equiv a(\bmod m)$的解会很困难。
求模7的二次剩余
若$m=7$,模$m$的完全剩余集合为{$1,2,3,4,5,6$}
$x^2\equiv 1(\bmod 7)$有解,$x=1,x=6$
$x^2\equiv 2(\bmod 7)$有解,$x=3,x=4$
$x^2\equiv 3(\bmod 7)$无解
$x^2\equiv 4(\bmod 7)$有解,$x=2,x=5$
$x^2\equiv 5(\bmod 7)$无解
$x^2\equiv 6(\bmod 7)$无解
由此可见1、2、4为模7的二次剩余,3、5、6是模7的非二次剩余
代数基础
群和环
群
- 群定义了一个二元运算的集合,这个二维运算可以表示为$\cdot$(具有一般性,可以指任何数学运算),群$G$记作{$G,\cdot$},$G$中的每一个序偶$(a,b)$通过运算生成$G$中的元素$(a\cdot b)$。
- 如果一个群的元素个数是有限的,则该群称为有限群。并且群的阶等于群中元素的个数。否则,称该群为无限群。
- 满足以下原则:
- 封闭性:如果$a$和$b$都属于$G$,则$a\cdot b$也属于$G$
- 结合律:对于$G$中的任何元素$a、b、c$都有$a\cdot (b\cdot c)=(a\cdot b)\cdot c$成立
- 单位元:$G$中存在一个元素$e$,对于$G$中任意元素$a$,都有$a\cdot e=e\cdot a=a$成立
- 逆元:对于$G$中任意元素$a$,$G$中都存在一个元素$a^{\prime}$,使得式$a\cdot a^{\prime}=a^{\prime}\cdot a=e$成立
- 交换律:对于$G$中的任意元素$a,b$,都有$a\cdot b=b\cdot a$成立
环
- 环是一个有两个二元运算的集合,记作{$R,+,\times$},这里两个二元运算分别是加法和乘法。从本质上来说,环就是一个集合,可以在其上进行加法、减法和乘法,而不脱离该集合。对于$R$中的任意元素$a、b、c$,满足以下公理:
- $R$关于加法是一个交换群,即满足群的全部5条原则。对于此种情况下的加法群,用0表示其单位元,$-a$表示$a$的加法逆元。
- 乘法的封闭性:如果$a$和$b$都属于$R$,则$ab$也属于$R$
- 乘法的结合律:对于$R$中任意元素$a、b、c$,$a(bc)=(ab)c$成立
- 分配律:对于$R$中的任意元素$a、b、c$,式$a(b+c)=ab+ac$和式$(a+b)c=ac+bc$总成立
- 乘法的交换律:对于$R$中的任意元素$a,b$,有$ab=ba$成立
- 乘法单位元:在$R$中存在元素1,是的对于$R$中的任意元素$a$,有$a1=1a=a$chengli
- 无零因子:如果有$R$中元素$a$和$b$,且$ab=0$,则必有$a=0$或$b=0$
内容更新中……